Note
Click here to download the full example code
Variational coordinate descent for Mixture of Gaussians¶
How to do Variational Bayes (VB) coordinate descent for GMM.
Here, we train a finite mixture of Gaussians with full covariances.
We’ll consider a mixture model with a symmetric Dirichlet prior:
as well as a standard conjugate prior on the mean and covariances, such that
We will initialize the approximate variational posterior using K=10 randomly chosen examples (‘randexamples’ procedure), and then perform coordinate descent updates (alternating local step and global step) until convergence.
# SPECIFY WHICH PLOT CREATED BY THIS SCRIPT IS THE THUMBNAIL IMAGE
# sphinx_gallery_thumbnail_number = 3
import bnpy
import numpy as np
import os
from matplotlib import pylab
import seaborn as sns
FIG_SIZE = (3, 3)
pylab.rcParams['figure.figsize'] = FIG_SIZE
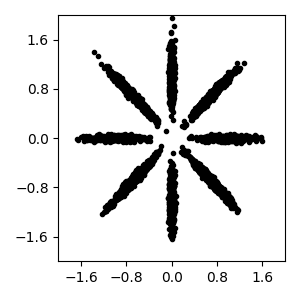
Read bnpy’s built-in “AsteriskK8” dataset from file.
dataset_path = os.path.join(bnpy.DATASET_PATH, 'AsteriskK8')
dataset = bnpy.data.XData.read_npz(
os.path.join(dataset_path, 'x_dataset.npz'))
Make a simple plot of the raw data
pylab.plot(dataset.X[:, 0], dataset.X[:, 1], 'k.')
pylab.gca().set_xlim([-2, 2])
pylab.gca().set_ylim([-2, 2])
pylab.tight_layout()
Training the model¶
Let’s do one single run of the VB algorithm.
Using 10 clusters and the ‘randexamples’ initializatio procedure.
trained_model, info_dict = bnpy.run(
dataset, 'FiniteMixtureModel', 'Gauss', 'VB',
output_path='/tmp/AsteriskK8/helloworld-K=10/',
nLap=100,
sF=0.1, ECovMat='eye',
K=10,
initname='randexamples')
Dataset Summary:
X Data
num examples: 5000
num dims: 2
Allocation Model: Finite mixture model. Dir prior param 1.00
Obs. Data Model: Gaussian with full covariance.
Obs. Data Prior: Gauss-Wishart on mean and covar of each cluster
E[ mean[k] ] =
[0. 0.]
E[ covar[k] ] =
[[0.1 0. ]
[0. 0.1]]
Initialization:
initname = randexamples
K = 10 (number of clusters)
seed = 1607680
elapsed_time: 0.0 sec
Learn Alg: VB | task 1/1 | alg. seed: 1607680 | data order seed: 8541952
task_output_path: /tmp/AsteriskK8/helloworld-K=10/1
1/100 after 0 sec. | 200.1 MiB | K 10 | loss 6.582634775e-01 |
2/100 after 0 sec. | 201.3 MiB | K 10 | loss 4.350235353e-01 | Ndiff 68.926
3/100 after 0 sec. | 201.3 MiB | K 10 | loss 3.454096950e-01 | Ndiff 193.565
4/100 after 0 sec. | 201.3 MiB | K 10 | loss 3.049230819e-01 | Ndiff 175.237
5/100 after 0 sec. | 201.3 MiB | K 10 | loss 2.732439109e-01 | Ndiff 108.630
6/100 after 0 sec. | 201.3 MiB | K 10 | loss 2.326372999e-01 | Ndiff 42.961
7/100 after 0 sec. | 201.3 MiB | K 10 | loss 2.100254570e-01 | Ndiff 9.814
8/100 after 0 sec. | 201.3 MiB | K 10 | loss 2.097453779e-01 | Ndiff 10.216
9/100 after 0 sec. | 201.3 MiB | K 10 | loss 2.094741199e-01 | Ndiff 10.608
10/100 after 0 sec. | 201.3 MiB | K 10 | loss 2.091535256e-01 | Ndiff 11.009
11/100 after 0 sec. | 201.3 MiB | K 10 | loss 2.087740779e-01 | Ndiff 11.403
12/100 after 0 sec. | 201.3 MiB | K 10 | loss 2.083262051e-01 | Ndiff 11.781
13/100 after 0 sec. | 201.3 MiB | K 10 | loss 2.078022512e-01 | Ndiff 12.135
14/100 after 0 sec. | 201.3 MiB | K 10 | loss 2.072001819e-01 | Ndiff 12.449
15/100 after 0 sec. | 201.3 MiB | K 10 | loss 2.065288318e-01 | Ndiff 12.706
16/100 after 0 sec. | 201.3 MiB | K 10 | loss 2.058118708e-01 | Ndiff 12.883
17/100 after 0 sec. | 201.3 MiB | K 10 | loss 2.050844132e-01 | Ndiff 12.951
18/100 after 0 sec. | 201.3 MiB | K 10 | loss 2.043795824e-01 | Ndiff 12.873
19/100 after 1 sec. | 201.3 MiB | K 10 | loss 2.037146182e-01 | Ndiff 12.598
20/100 after 1 sec. | 201.3 MiB | K 10 | loss 2.030678434e-01 | Ndiff 12.069
21/100 after 1 sec. | 201.3 MiB | K 10 | loss 2.022621299e-01 | Ndiff 11.232
22/100 after 1 sec. | 201.3 MiB | K 10 | loss 2.008648784e-01 | Ndiff 10.057
23/100 after 1 sec. | 201.3 MiB | K 10 | loss 2.002168334e-01 | Ndiff 8.536
24/100 after 1 sec. | 201.3 MiB | K 10 | loss 1.995420809e-01 | Ndiff 8.587
25/100 after 1 sec. | 201.3 MiB | K 10 | loss 1.988594991e-01 | Ndiff 9.312
26/100 after 1 sec. | 201.3 MiB | K 10 | loss 1.982035545e-01 | Ndiff 9.984
27/100 after 1 sec. | 201.3 MiB | K 10 | loss 1.974254707e-01 | Ndiff 10.598
28/100 after 1 sec. | 201.3 MiB | K 10 | loss 1.966834121e-01 | Ndiff 11.131
29/100 after 1 sec. | 201.3 MiB | K 10 | loss 1.964267444e-01 | Ndiff 11.549
30/100 after 1 sec. | 201.3 MiB | K 10 | loss 1.961250819e-01 | Ndiff 11.802
31/100 after 1 sec. | 201.3 MiB | K 10 | loss 1.957730227e-01 | Ndiff 11.830
32/100 after 1 sec. | 201.3 MiB | K 10 | loss 1.953666781e-01 | Ndiff 11.565
33/100 after 1 sec. | 201.3 MiB | K 10 | loss 1.949058031e-01 | Ndiff 10.930
34/100 after 1 sec. | 201.3 MiB | K 10 | loss 1.943977009e-01 | Ndiff 9.860
35/100 after 1 sec. | 201.3 MiB | K 10 | loss 1.938623040e-01 | Ndiff 8.334
36/100 after 1 sec. | 201.3 MiB | K 10 | loss 1.933345511e-01 | Ndiff 6.449
37/100 after 1 sec. | 201.3 MiB | K 10 | loss 1.928570776e-01 | Ndiff 4.458
38/100 after 1 sec. | 201.3 MiB | K 10 | loss 1.924667495e-01 | Ndiff 2.727
39/100 after 1 sec. | 201.3 MiB | K 10 | loss 1.921899371e-01 | Ndiff 1.530
40/100 after 1 sec. | 201.3 MiB | K 10 | loss 1.919922352e-01 | Ndiff 0.873
41/100 after 1 sec. | 201.3 MiB | K 10 | loss 1.916267958e-01 | Ndiff 0.492
42/100 after 1 sec. | 201.3 MiB | K 10 | loss 1.909787395e-01 | Ndiff 0.045
... done. converged.
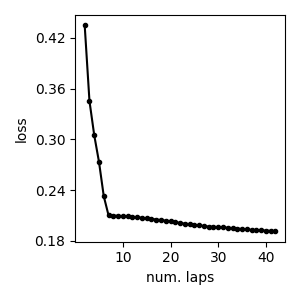
Loss function trace plot¶
We can plot the value of the loss function over iterations, starting after the first full pass over the dataset (first lap).
As expected, we see monotonic decrease in the loss function’s score after every subsequent iteration.
Remember that the VB algorithm for GMMs is guaranteed to decrease this loss function after every step.
pylab.plot(info_dict['lap_history'][1:], info_dict['loss_history'][1:], 'k.-')
pylab.xlabel('num. laps')
pylab.ylabel('loss')
pylab.tight_layout()
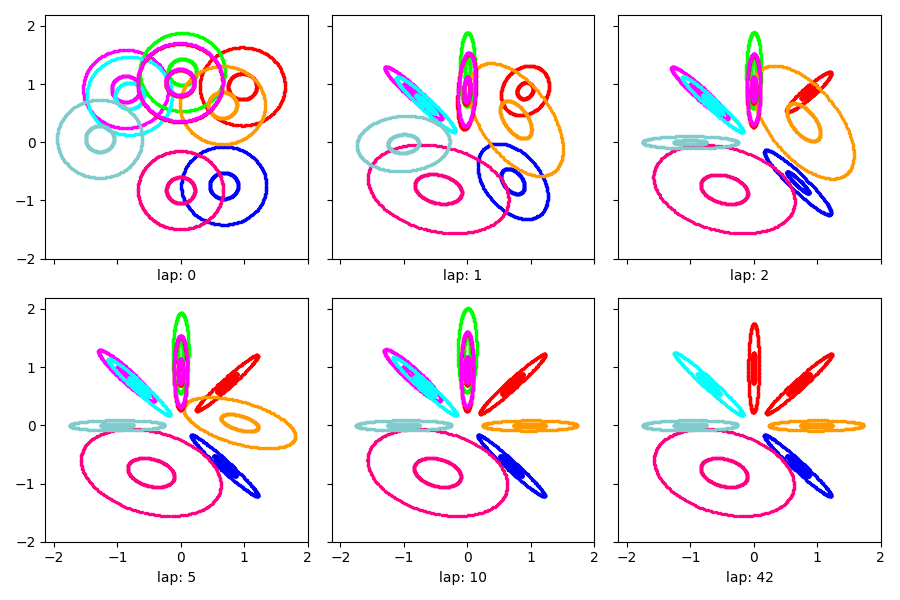
Visualization of learned clusters¶
Here’s a short function to show the learned clusters over time.
def show_clusters_over_time(
task_output_path=None,
query_laps=[0, 1, 2, 5, 10, None],
nrows=2):
''' Read model snapshots from provided folder and make visualizations
Post Condition
--------------
New matplotlib plot with some nice pictures.
'''
ncols = int(np.ceil(len(query_laps) // float(nrows)))
fig_handle, ax_handle_list = pylab.subplots(
figsize=(FIG_SIZE[0] * ncols, FIG_SIZE[1] * nrows),
nrows=nrows, ncols=ncols, sharex=True, sharey=True)
for plot_id, lap_val in enumerate(query_laps):
cur_model, lap_val = bnpy.load_model_at_lap(task_output_path, lap_val)
# Plot the current model
cur_ax_handle = ax_handle_list.flatten()[plot_id]
bnpy.viz.PlotComps.plotCompsFromHModel(
cur_model, Data=dataset, ax_handle=cur_ax_handle)
cur_ax_handle.set_xticks([-2, -1, 0, 1, 2])
cur_ax_handle.set_yticks([-2, -1, 0, 1, 2])
cur_ax_handle.set_xlabel("lap: %d" % lap_val)
pylab.tight_layout()
Show the estimated clusters over time
show_clusters_over_time(info_dict['task_output_path'])
SKIPPED 3 comps with size below 0.00
Total running time of the script: ( 0 minutes 1.888 seconds)